一：基础入门与算法分析

1. 核心概念

  • 数据结构: 一门研究如何有效组织数据，以提高数据处理效率的学科。它关注数据间的逻辑关系（逻辑结构）和在计算机中的存储方式（存储形式）。
  • 逻辑结构: 指数据元素之间的内在关系，与存储方式无关。常见有：
    • 线性结构: 元素间为一对一关系 (如：线性表、栈、队列)。
    • 非线性结构: 元素间为一对多或多对多关系 (如：树、图)。
  • 存储形式 (物理结构): 指数据在内存中的存储方式。主要有：
    • 顺序存储: 将逻辑上相邻的元素存储在物理位置也相邻的存储单元中（如：数组）。
    • 链式存储: 物理位置不一定相邻，通过指针来表示元素间的逻辑关系（如：链表）。

[info] 核心思想

逻辑结构是“战略”，决定了数据应该如何组织；存储结构是“战术”，决定了数据具体如何存放。一种逻辑结构可以有多种存储实现。

2. 算法性能分析

算法分析旨在评估算法的优劣，主要考量两个维度：时间复杂度和空间复杂度。目标是让程序运行得更快，占用内存更少。

时间复杂度

  • 概念: 衡量算法执行时间随数据规模增长而变化的趋势，通常不考察绝对时间，而是估算基本操作的执行次数（语句频度）。

  • 表示法: 使用大O表示法 O()，只关注最高次幂项，忽略常数和低次幂项。

    （为什么只关注最大的？看这个视频：）

  • 示例:

    1
    2
    3
    4
    5
    6
    7
    8
    9
    void func(int n) {
        // 执行 n 次
        for (int i = 0; i < n; i++) { 
            // 执行 n*n 次
            for (int j = 0; j < n; j++) {
                printf("Hello\n");
            }
        }
    }

    上述代码总执行次数为 n * n = n^2。因此，时间复杂度为 O(n²)。


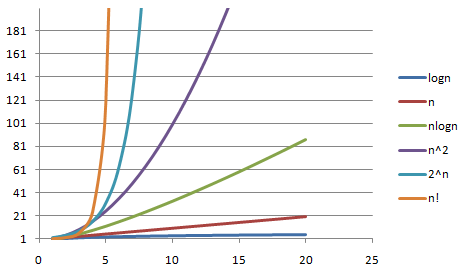
不同时间复杂度的增长趋势对比

空间复杂度

  • 概念: 衡量算法在运行过程中临时占用存储空间大小的量度，同样采用大O表示法。

时空互换

  • 概念: 在某些场景下，可以通过增加空间消耗来换取更短的执行时间（空间换时间），或者通过增加计算时间来减少内存占用（时间换空间）。

  • 案例实战：快速计算二进制中1的位数

    • 问题: 给定一个int，要求“尽快”求出其二进制表示中1的个数。

    • 常规解法 (时间换空间): 循环移位或与操作，逐位判断。

      1
      2
      3
      4
      5
      6
      7
      8
      int count_ones(unsigned int n) {
          int count = 0;
          while (n > 0) {
              n &= (n - 1); // 每次操作消除最右边的1
              count++;
          }
          return count;
      }

    • 高效解法 (空间换时间): 预计算。创建一个256大小的数组，存储0-255每个数包含的1的个数。对于32位整数，分4个字节查表相加即可。

      1
      2
      3
      4
      5
      6
      7
      8
      9
      10
      11
      12
      13
      14
      // 全局预计算表
      int bits_in_char[256]; 
      void precompute() {
          for (int i = 0; i < 256; i++) {
              bits_in_char[i] = (i & 1) + bits_in_char[i / 2];
          }
      }

      int count_ones_fast(unsigned int n) {
          return bits_in_char[n & 0xff] + 
                 bits_in_char[(n >> 8) & 0xff] +
                 bits_in_char[(n >> 16) & 0xff] +
                 bits_in_char[(n >> 24) & 0xff];
      }

      这是一种典型的用内存空间（bits_in_char数组）换取固定时间（4次查表+3次加法）的策略。

二：线性表

线性表是数据结构世界的基础构件，其两种主要实现——顺序表和链表，在性能上各有取舍，适用于完全不同的场景。

3. 顺序表

  • 定义: 使用一段连续的物理内存来存储逻辑上相邻的数据元素。在C语言中，其最直接的体现就是数组。
  • 优点:
    • 随机访问 O(1): 可通过下标直接访问任何元素，速度极快。
    • 存储密度高: 无需额外空间存储元素间的关系。
  • 缺点:
    • 插入/删除 O(n): 在中间或头部操作，需要移动大量元素。
    • 空间不灵活: 容量固定，扩容成本高或实现复杂。
  • 适用场景: 数据量相对稳定，读操作远多于写操作的场景，如配置表、静态数据集等。

4. 链表

问题引入：为什么普通链表不够用？

我们先看一个普通的学生信息单链表节点：

1
2
3
4
5
struct student {
    char name[20];
    int id;
    struct student *next; // 指针域耦合了数据类型
};

这个设计存在一个致命缺陷：缺乏通用性。next指针的类型是struct student *，这意味着为student链表编写的所有操作函数（如insert_student, remove_student），都无法用于管理teacher或其他任何类型的链表。在像Linux内核这样拥有成千上万种数据结构的复杂项目中，为每种结构都重写一套链表代码是不可接受的。

设计哲学：Linux内核的解决方案——数据与逻辑分离

Linux内核-内核链表

Linux内核用一种极其巧妙的方式解决了这个问题：将**“链”的逻辑从“数据”本身**中抽离。

  1. 定义一个“纯粹”的链表节点: 创建一个不包含任何业务数据，只负责链接的通用节点结构struct list_head。

    1
    2
    3
    4
    // From <linux/list.h>
    struct list_head {
        struct list_head *next, *prev;
    };

    这是一个标准的双向循环链表节点。

  2. “寄生”于用户数据结构: 将这个list_head结构作为一个成员，嵌入到任何需要被链式管理的用户数据结构中。

    1
    2
    3
    4
    5
    6
    7
    struct student {
        // --- 用户数据域 ---
        char name[20];
        int id;
        // --- 链表逻辑域 ---
        struct list_head list; // "寄生"的内核链表节点
    };

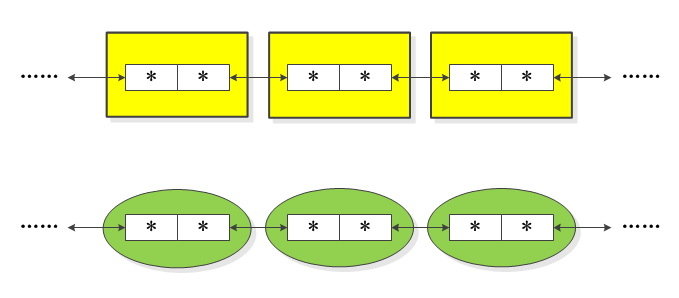
将标准链表节点嵌入用户数据结构

难点攻克：如何从“链”找到“数据”？

所有链表API操作的都是list_head指针，但我们最终需要的是包含业务数据的student结构体。如何从list成员的地址反向推算出其“宿主”student结构体的起始地址？

这就是内核链表最核心的宏 list_entry 的作用。

  • 原理: 宿主结构体地址 = 成员地址 - 成员在宿主结构体中的偏移量

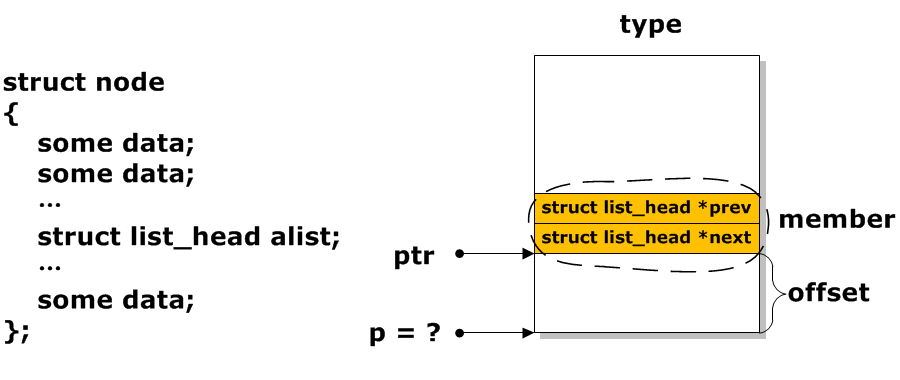
通过成员地址和偏移量计算宿主地址

  • C语言实现:

    1
    2
    # define list_entry(ptr, type, member) \
         ((type *)((char *)(ptr) - (unsigned long)(&((type *)0)->member)))
    • ptr: 指向list_head成员的指针。
    • type: 宿主结构体的类型 (如 struct student)。
    • member: list_head成员在宿主结构体中的名字 (如 list)。
    • &((type *)0)->member: 这是一个编译时技巧，计算出member在type结构体中的偏移量。

代码实战：使用内核链表管理学生信息

以下是一个完整的、可编译的示例，演示如何使用内核链表API。
(为方便使用，已将内核的list.h相关宏和函数提取整理)

kernel_list.h (简化版)

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
#ifndef _KERNEL_LIST_H
#define _KERNEL_LIST_H

// 1. 核心节点定义
struct list_head {
    struct list_head *next, *prev;
};

// 2. 初始化宏
#define LIST_HEAD_INIT(name) { &(name), &(name) }
#define LIST_HEAD(name) struct list_head name = LIST_HEAD_INIT(name)
static inline void INIT_LIST_HEAD(struct list_head *list) {
    list->next = list;
    list->prev = list;
}

// 3. 核心辅助函数 (内部使用)
static inline void __list_add(struct list_head *new,
                              struct list_head *prev,
                              struct list_head *next) {
    next->prev = new;
    new->next = next;
    new->prev = prev;
    prev->next = new;
}

// 4. 对外API: 添加节点
static inline void list_add(struct list_head *new, struct list_head *head) {
    __list_add(new, head, head->next); // 头插
}
static inline void list_add_tail(struct list_head *new, struct list_head *head) {
    __list_add(new, head->prev, head); // 尾插
}

// 5. 核心宏：获取宿主结构体
#define list_entry(ptr, type, member) \
    ((type *)((char *)(ptr) - (unsigned long)(&((type *)0)->member)))

// 6. 对外API: 遍历
#define list_for_each_entry(pos, head, member) \
    for (pos = list_entry((head)->next, typeof(*pos), member); \
         &pos->member != (head); \
         pos = list_entry(pos->member.next, typeof(*pos), member))

#endif

main.c

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
#include <stdio.h>
#include <stdlib.h>
#include <string.h>
#include "kernel_list.h"

// 用户数据结构
struct student {
    int id;
    char name[32];
    struct list_head list; // 嵌入内核链表节点
};

int main() {
    // 1. 创建并初始化链表头 (这是一个独立的头结点)
    LIST_HEAD(student_list);

    // 2. 添加学生信息
    printf("Adding students...\n");
    struct student *stu1 = malloc(sizeof(struct student));
    stu1->id = 101;
    strcpy(stu1->name, "Alice");
    list_add_tail(&stu1->list, &student_list); // 尾插

    struct student *stu2 = malloc(sizeof(struct student));
    stu2->id = 102;
    strcpy(stu2->name, "Bob");
    list_add_tail(&stu2->list, &student_list);

    // 3. 遍历链表并打印信息
    printf("\n--- Student List ---\n");
    struct student *iter;
    list_for_each_entry(iter, &student_list, list) {
        printf("ID: %d, Name: %s\n", iter->id, iter->name);
    }

    // 4. 查找并释放Bob的信息 (演示删除)
    printf("\nFinding and removing Bob (ID 102)...\n");
    struct student *temp;
    list_for_each_entry_safe(iter, temp, &student_list, list) { // 安全遍历，因为要删除
        if (iter->id == 102) {
            list_del(&iter->list); // 从链表中脱离
            free(iter);            // 释放内存
            printf("Bob removed.\n");
        }
    }
    
    printf("\n--- Updated Student List ---\n");
    list_for_each_entry(iter, &student_list, list) {
        printf("ID: %d, Name: %s\n", iter->id, iter->name);
    }
    
    // ... 在程序结束时需要遍历并释放所有剩余节点
    return 0;
}

内核链表精髓总结

  • 通用性: 一套API，管理所有类型的数据。
  • 高效性: 增删操作为 O(1)，无数据拷贝。
  • 健壮性: 经过Linux内核数十年验证，稳定可靠。
  • 思想: 完美的“控制反转”，用户只需关注自己的数据，将组织逻辑交给标准库。

代码实战：单链表的反转

掌握了链表的创建和遍历后，一个最经典的面试题和算法练习便是——反转一个单向链表。

例如，将 1 -> 2 -> 3 -> 4 -> 5 变为 5 -> 4 -> 3 -> 2 -> 1。

1. 核心挑战

在遍历链表时，每个节点只知道自己的“下一个”是谁。当我们想让 节点2 指向 节点1 时，一旦执行 2->next = 1，我们就会立即丢失通往 节点3 的路径。因此，算法设计的关键在于：在修改指针前，如何保存好“未来的路”。

2. 算法本质 - 三个职责的流转

无论代码怎么写，任何正确的迭代反转算法，都必须在循环的每一步中，清晰地管理好三个核心的“状态职责”：

  1. Current (当前): 指向当前正要被反转指向的节点。
  2. Reversed (已反转): 指向已经反转好的新链表的头部。
  3. Upcoming (未反转): 指向Current在原始链表中的下一个节点，作为“路标”以防断链。

算法的每一步，就是这三个职责在指针变量之间的一次优雅“交谊舞”。

3. 思想的多种代码表达

表达一：标准三指针迭代法 (教科书式)

这是最常见、最清晰的实现。我们用三个独立的指针变量来分别扮演这三个角色。

  • p_rev: 扮演 Reversed 角色。
  • p_cur: 扮演 Current 角色。
  • p_upc: 扮演 Upcoming 角色。
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
void reverse_list(linklist head) {
    if (head == NULL || head->next == NULL) return;

    linklist p_rev = NULL;
    linklist p_cur = head->next;
    linklist p_upc = NULL;

    while (p_cur != NULL) {
        // 1. 保存未来: Upcoming 指针记住 Current 的下一个节点
        p_upc = p_cur->next;

        // 2. 反转当前: Current 指向已反转链表的头部
        p_cur->next = p_rev;

        // 3. 前进迭代: 更新 Reversed 和 Current 的角色
        p_rev = p_cur;
        p_cur = p_upc;
    }
    
    // 4. 收尾: 将头结点指向反转后的新头
    head->next = p_rev;
}

深度思考：通过严谨的排列组合，我们可以证明，只要有三个指针变量，无论哪个变量扮演哪个角色（共 3! = 6 种组合），其核心的四步操作逻辑是完全一致的，都能写出正确的算法。

表达二：头插法 (巧妙利用头结点)

这种方法更加精炼，它巧妙地让“头结点”本身参与到算法中，扮演 Reversed 的角色。

  • p_cur: 扮演 Current。
  • p_upc: 扮演 Upcoming。
  • head->next: 扮演 Reversed 的角色，始终指向新链表的头。
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
void reverse_list_head_insertion(linklist head) {
    if (head == NULL || head->next == NULL) return;
    
    linklist p_cur = head->next;
    linklist p_upc = NULL;

    // 先将头结点与原链表断开，它将作为新链表的“锚点”
    head->next = NULL;

    while (p_cur != NULL) {
        // 1. 保存未来
        p_upc = p_cur->next;
        
        // 2. 反转当前 (头插法核心)
        //    让当前节点指向新链表的头 (即 head->next)
        p_cur->next = head->next; 
        //    更新新链表的头为当前节点
        head->next = p_cur;

        // 3. 前进迭代
        p_cur = p_upc;
    }
}
表达三：递归法 (时空转换的艺术)

递归将迭代的循环逻辑转换为了函数调用栈的递进与回溯，代码极简，但对理解的要求更高。

  • 递进 (Drill Down): 函数不断调用自身，直到链表末尾。这个过程本身就“记住”了返回的路径。
  • 回溯 (Roll Back): 从链表末尾开始，在每一层函数返回时，将当前层的节点指针反转。
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
// 辅助递归函数
linklist reverse_recursive_helper(linklist current) {
    // 基本情况：到达链表尾部，返回新的头节点
    if (current == NULL || current->next == NULL) {
        return current;
    }
    
    // 递进：假设后面的部分已经反转好，并拿到新头
    linklist new_head = reverse_recursive_helper(current->next);
    
    // 回溯时的操作：反转指针
    current->next->next = current;
    current->next = NULL;
    
    return new_head;
}

void reverse_list_recursive(linklist head) {
    if (head == NULL) return;
    head->next = reverse_recursive_helper(head->next);
}

思维体操总结

  • 算法的“道”与“术”: 链表反转的“道”是管理好Current, Reversed, Upcoming三个状态。而迭代法、头插法、递归法则是实现这个“道”的不同“术”。
  • 没有“碰巧”的正确: 即使写出一个非主流但可行的算法，也绝非巧合，而是无意中构建了一套逻辑自洽的状态流转系统。理解其内在逻辑，比死记标准答案更有价值。
  • 代码是思想的投影: 同一个算法思想，可以有多种代码表达。探索这些不同表达方式的优劣和内在联系，是提升编程内功的关键。

代码实战：约瑟夫环

在掌握了链表的增删改查之后，约瑟夫环问题是另一个绝佳的综合性练习，它完美地融合了循环链表的构建与节点的规律性删除。

问题描述：n 个人（编号 1 到 n）围成一个圈。从第 1 个人开始报数，报到 m 的那个人出列，他的下一个人又从 1 开始报数，报到 m 的那个人再次出列……如此循环，直到所有人出列。请找出最后一个出列的人，或者按顺序输出出列人的序列。

为了解决这个问题，单向循环链表是天然的数据结构。

1. 算法分析与实现

约瑟夫环的核心操作只有两步，循环往复：

  1. “走”：从当前节点开始，向后移动 m-1 步，找到那个“倒霉蛋”的前一个节点。
  2. “删”：将“倒霉蛋”从环中移除，并释放其内存。

算法持续进行，直到环中只剩下一个节点。

2. C语言代码实现

下面是一个完整的、可编译的约瑟夫环问题解决方案。程序会要求输入总人数 n 和报数阈值 m，然后模拟整个过程。

linklist.h (头文件)

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
#ifndef __LINKLIST_H
#define __LINKLIST_H

#include <stdio.h>
#include <stdlib.h>

// 链表节点定义
typedef struct node {
  int data;           // 节点数据 (人的编号)
  struct node *next;
} listnode, *linklist;

// 函数声明
linklist create_josephus_ring(int n);
void show_list(linklist head);
void solve_josephus(linklist head, int m);

#endif

main.c (主程序)

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
#include "linklist.h"

int main(void) {
  int n, m;

  printf("请输入总人数 n: ");
  scanf("%d", &n);
  printf("请输入报数阈值 m: ");
  scanf("%d", &m);

  if (n < 1 || m < 1) {
    printf("输入无效，人数和报数阈值必须大于0。\n");
    return 1;
  }

  // 1. 创建约瑟夫环
  printf("\n正在创建包含 %d 人的约瑟夫环...\n", n);
  linklist ring_head = create_josephus_ring(n);
  printf("初始环: ");
  show_list(ring_head);

  // 2. 开始模拟并解决问题
  printf("\n开始淘汰过程 (报数为 %d 的人出列):\n", m);
  solve_josephus(ring_head, m);

  return 0;
}

linklist.c (函数实现)

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83
84
85
86
87
88
89
90
91
92
#include "linklist.h"

// 创建一个包含 n 个节点的单向循环链表 (约瑟夫环)
linklist create_josephus_ring(int n) {
    if (n < 1) return NULL;

    linklist head = NULL, tail = NULL;

    for (int i = 1; i <= n; i++) {
        // 创建新节点
        linklist new_node = malloc(sizeof(listnode));
        if (new_node == NULL) {
            perror("创建节点失败");
            exit(1);
        }
        new_node->data = i;

        if (head == NULL) {
            // 第一个节点
            head = new_node;
            tail = new_node;
        } else {
            // 尾插法
            tail->next = new_node;
            tail = new_node;
        }
    }
    // 将链表头尾相连，形成环
    tail->next = head;
    
    return head;
}

// 遍历并打印循环链表
void show_list(linklist head) {
    if (head == NULL) {
        printf("链表为空\n");
        return;
    }
    linklist p = head;
    do {
        printf("%d ", p->data);
        p = p->next;
    } while (p != head);
    printf("\n");
}

// 解决约瑟夫环问题
void solve_josephus(linklist head, int m) {
    if (head == NULL) return;
    
    // 如果 m=1，特殊处理，避免在原地打转
    if (m == 1) {
        linklist p = head;
        while(p->next != p) {
            printf("%d出列. ", p->data);
            linklist temp = p->next;
            // 找到p的前一个节点
            linklist prev = p;
            while(prev->next != p) prev = prev->next;
            prev->next = p->next;
            free(p);
            p = temp;
        }
        printf("\n最后幸存者是: %d\n", p->data);
        free(p);
        return;
    }

    linklist current = head;
    while (current->next != current) { // 循环直到只剩一个节点
        // 1. "走": 找到被杀节点的前一个节点
        //    因为要找第 m 个，所以需要走 m-2 步 (从当前节点之后开始数)
        for (int i = 1; i < m - 1; i++) {
            current = current->next;
        }

        // 2. "删": 删除目标节点
        linklist kill_node = current->next;
        printf("%d出列. ", kill_node->data);
        
        // 从环中移除
        current->next = kill_node->next;
        free(kill_node);

        // 3. 更新下一次报数的起点
        current = current->next;
    }
    
    printf("\n\n最后幸存者是: %d\n", current->data);
    free(current); // 释放最后一个节点
}

约瑟夫环问题总结

  • 数据结构选择: 循环链表是该问题最直观、最自然的模型。
  • 算法核心: 关键在于定位到待删除节点的前一个节点，这是安全删除链表节点的通用法则。
  • 指针操作: 每次删除操作后，必须小心地更新当前指针（下一轮的起始点），确保逻辑链条不断裂。
  • 边界情况: 考虑 n=1 或 m=1 等特殊情况，能体现代码的健壮性。例如，当 m=1 时，每次都删除当前节点，指针移动的逻辑需要特别处理。

三：树形结构

二叉搜索树（BST）是利用树结构实现高效查找的典范。它的核心在于维持一个严格的有序性。

5. 二叉搜索树核心特性

  • 定义: 对于树中任意节点，其左子树所有节点的值都小于该节点，其右子树所有节点的值都大于该节点。
  • 价值: 平均情况下，查找、插入、删除操作的时间复杂度均为 O(log n)，效率远超线性表的 O(n)。

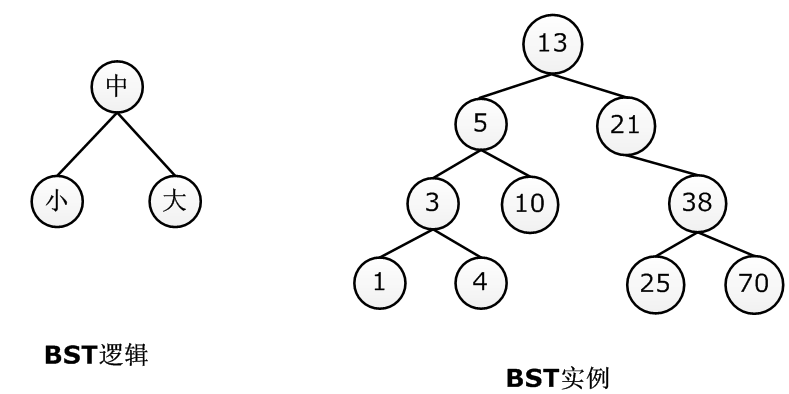
6. 难点攻克：二叉树的删除操作

BST的插入相对简单，只需遵循规则找到空位即可。而删除操作则要复杂得多，因为它必须在删除节点后维持BST的有序性。

删除节点 x 的三种情况分析：

  1. x 是叶子节点: 最简单的情况，直接删除 x，并将其父节点的相应指针置为NULL。
  2. x 只有一个子节点 (左或右): 将 x 的父节点直接链接到 x 的唯一子节点上，然后释放 x。
  3. x 有两个子节点: 这是最复杂的情况。不能简单删除，否则会断开其两棵子树。
    • 解决策略: 在x的子树中找到一个合适的“替身”来取代x的位置。这个替身有两个选择：
      • 前驱 (predecessor): x 左子树中的最大值。
      • 后继 (successor): x 右子树中的最小值。
    • 操作步骤 (以后继为例):
      a. 在 x 的右子树中，一路向左，找到最小值节点 s (后继)。
      b. 将 s 的值赋给 x。
      c. 问题转化为在 x 的右子树中删除节点 s。由于 s 是最小值，它最多只有一个右孩子，问题降级为情况1或情况2。

图解删除双子节点 (删除节点 8)

假设我们要删除根节点 8：


1. 目标：删除节点 8。

a. 找到 8 的后继：在右子树 {10, 14, 13} 中找到最小值，即 10。


2. 找到后继节点 10。

b. 用后继 10 的值覆盖 8。


3. 用后继的值覆盖待删除节点。

c. 在原右子树中删除后继 10。此时 10 的删除操作属于情况2（它有一个右孩子 14），将其父节点(现在是新的根10)直接链接到其子节点 14。


4. 递归删除后继节点，完成重构。

代码实现：二叉树删除

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
typedef struct node {
    int data;
    struct node *lchild, *rchild;
} bstNode;

// 辅助函数：查找子树中的最小值节点
bstNode* findMin(bstNode* root) {
    if (root == NULL) return NULL;
    while (root->lchild != NULL) {
        root = root->lchild;
    }
    return root;
}

// BST 删除函数
bstNode* bstRemove(bstNode* root, int data) {
    // 1. 基线条件：树为空或未找到
    if (root == NULL) return root;

    // 2. 递归查找
    if (data < root->data) {
        root->lchild = bstRemove(root->lchild, data);
    } else if (data > root->data) {
        root->rchild = bstRemove(root->rchild, data);
    } else { // 3. 找到了要删除的节点
        // 情况1: 叶子节点 或 情况2: 单子节点
        if (root->lchild == NULL) {
            bstNode *temp = root->rchild;
            free(root);
            return temp;
        } else if (root->rchild == NULL) {
            bstNode *temp = root->lchild;
            free(root);
            return temp;
        }

        // 情况3: 双子节点
        // 找到右子树的最小值 (后继)
        bstNode *temp = findMin(root->rchild);
        // 用后继的值覆盖当前节点
        root->data = temp->data;
        // 在右子树中递归删除那个后继节点
        root->rchild = bstRemove(root->rchild, temp->data);
    }
    return root;
}

[!WARNING] 二叉树的退化风险
如果插入的数据是预先有序或基本有序的，BST会退化成一个倾斜的链表，所有操作的性能将从 O(log n) 急剧下降到 O(n)。这正是**平衡二叉树（如AVL树、红黑树）**存在的意义。

四：栈与队列

栈和队列虽然在操作上受到限制，但正是这种限制赋予了它们独特的“先进后出”(LIFO)和“先进先出”(FIFO)特性，使其成为解决特定问题的强大工具。

7. 栈

  • 核心特性: 后进先出 (Last-In, First-Out)。最后压入栈的元素，最先被弹出。
  • 应用场景:
    1. 函数调用与递归: 这是栈最经典的应用。每次函数调用，其上下文（参数、返回地址、局部变量）被压入一个系统维护的“调用栈”。函数返回时，从栈顶弹出其上下文。递归本质上是函数调用自身的特例。
    2. 表达式求值: 将中缀表达式转换为后缀表达式（逆波兰表示法），然后使用栈进行求值。
    3. 括号匹配: 遍历字符串，遇到左括号就入栈，遇到右括号就检查栈顶是否为匹配的左括号，若是则出栈，否则不匹配。
    4. 深度优先搜索 (DFS): 在图或树的遍历中，DFS的递归实现天然利用了调用栈。其迭代实现则需要手动维护一个栈来存储待访问的节点。

实战案例：括号匹配

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
#include <stdio.h>
#include <stdlib.h>
#include <stdbool.h>
#include <string.h>

// 简单的链式栈实现
typedef struct StackNode {
    char data;
    struct StackNode *next;
} StackNode;

void push(StackNode** top, char data) {
    StackNode* newNode = (StackNode*)malloc(sizeof(StackNode));
    newNode->data = data;
    newNode->next = *top;
    *top = newNode;
}

bool pop(StackNode** top, char* data) {
    if (*top == NULL) return false;
    StackNode* temp = *top;
    *data = temp->data;
    *top = temp->next;
    free(temp);
    return true;
}

// 核心匹配逻辑
bool areBracketsBalanced(char* expr) {
    StackNode* stack = NULL;
    char popped_char;

    for (int i = 0; i < strlen(expr); i++) {
        if (expr[i] == '(' || expr[i] == '[' || expr[i] == '{') {
            push(&stack, expr[i]);
            continue;
        }

        // 如果遇到右括号但栈为空，则不匹配
        if (stack == NULL) return false;

        switch (expr[i]) {
            case ')':
                pop(&stack, &popped_char);
                if (popped_char != '(') return false;
                break;
            case ']':
                pop(&stack, &popped_char);
                if (popped_char != '[') return false;
                break;
            case '}':
                pop(&stack, &popped_char);
                if (popped_char != '{') return false;
                break;
        }
    }

    // 如果遍历完，栈中还有剩余的左括号，则不匹配
    return (stack == NULL);
}

int main() {
    char expr1[] = "{()}[]";
    char expr2[] = "([)]";
    printf("%s is %s\n", expr1, areBracketsBalanced(expr1) ? "balanced" : "not balanced");
    printf("%s is %s\n", expr2, areBracketsBalanced(expr2) ? "balanced" : "not balanced");
    return 0;
}

8. 队列 (Queue)：FIFO的应用

  • 核心特性: 先进先出 (First-In, First-Out)。最先进入队列的元素，最先被移出。
  • 应用场景:
    1. 资源调度: 操作系统中的任务调度、打印机任务队列等，需要公平地处理请求，先到先服务。
    2. 广度优先搜索 (BFS): 在图或树的遍历中，BFS使用队列来存储待访问的节点，保证按层级顺序进行访问。
    3. 缓冲区 (Buffer): 在生产者-消费者模型中，队列作为缓冲区，平衡生产者和消费者之间速度不匹配的问题。
    4. 网络数据包排队: 路由器处理数据包时，通常将其放入队列中，按到达顺序转发。

实战案例：树的层序遍历 (BFS)

层序遍历是广度优先搜索在树上的直接应用，其核心就是队列。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
// 假设已存在BST的节点定义 bstNode 和一个简单的队列实现
// queue.h (包含enQueue, deQueue, isQueueEmpty等函数)

void levelOrderTraversal(bstNode* root) {
    if (root == NULL) return;

    // 1. 创建一个队列并把根节点入队
    Queue* q = createQueue();
    enQueue(q, root);

    while (!isQueueEmpty(q)) {
        // 2. 从队列中取出一个节点
        bstNode* current = deQueue(q);
        printf("%d ", current->data);

        // 3. 将该节点的非空子节点入队
        if (current->lchild != NULL) {
            enQueue(q, current->lchild);
        }
        if (current->rchild != NULL) {
            enQueue(q, current->rchild);
        }
    }
    printf("\n");
}

五：排序算法

排序是计算机科学中最基础也最重要的操作之一。选择合适的排序算法对程序性能至关重要。

9. 快速排序

快速排序是实践中平均性能最好的排序算法，其精髓在于分治思想和高效的**分区（Partition）**操作。

难点攻克：partition函数的多种实现

partition函数的目标是：选择一个基准（pivot），并将数组划分为两部分，使得左边的都小于等于基准，右边的都大于等于基准，最后返回基准的最终位置。

实现一：Lomuto 分区方案 (易于理解)

  • 思路:
    1. 选择最后一个元素作为pivot。
    2. 维护一个指针i，指向“小于等于pivot”区域的末尾。
    3. 遍历数组（除pivot外），如果发现元素arr[j]小于等于pivot，则将i后移一位，并交换arr[i]和arr[j]。
    4. 最后，将pivot（原arr[high]）与arr[i+1]交换。
1
2
3
4
5
6
7
8
9
10
11
12
13
14
// Lomuto partition scheme
int partition_lomuto(int arr[], int low, int high) {
    int pivot = arr[high]; // 选择最后一个元素为基准
    int i = (low - 1);     // 小于等于pivot区域的边界

    for (int j = low; j <= high - 1; j++) {
        if (arr[j] <= pivot) {
            i++;
            swap(&arr[i], &arr[j]);
        }
    }
    swap(&arr[i + 1], &arr[high]);
    return (i + 1);
}

实现二：Hoare 分区方案 (原始方案，效率更高)

  • 思路:
    1. 选择第一个元素作为pivot。
    2. 使用两个指针i和j，分别从数组的两端向中间扫描。
    3. i向右扫描，直到找到一个大于pivot的元素。
    4. j向左扫描，直到找到一个小于pivot的元素。
    5. 交换arr[i]和arr[j]。
    6. 重复3-5步，直到i和j交错。
  • 注意: Hoare方案最后返回的不一定是pivot的最终位置，而是划分的分界点。
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
// Hoare partition scheme
int partition_hoare(int arr[], int low, int high) {
    int pivot = arr[low];
    int i = low - 1;
    int j = high + 1;

    while (1) {
        // 从左向右找第一个大于等于pivot的元素
        do { i++; } while (arr[i] < pivot);
        // 从右向左找第一个小于等于pivot的元素
        do { j--; } while (arr[j] > pivot);

        // 如果指针交错，则分区完成
        if (i >= j) return j;

        swap(&arr[i], &arr[j]);
    }
}

完整的快速排序实现 (使用Lomuto)

1
2
3
4
5
6
7
8
9
10
void quickSort(int arr[], int low, int high) {
    if (low < high) {
        // pi 是分区后基准元素的索引
        int pi = partition_lomuto(arr, low, high);

        // 递归地对基准左右两边的子数组进行排序
        quickSort(arr, low, pi - 1);
        quickSort(arr, pi + 1, high);
    }
}

10. 归并排序

归并排序同样基于分治思想，但其核心操作是**归并（Merge）**而非分区。

  • 核心思想:
    1. 分解 (Divide): 将数组递归地对半切分，直到每个子数组只有一个元素（天然有序）。
    2. 合并 (Conquer): 将相邻的两个有序子数组合并成一个更大的有序数组。

难点攻克：merge函数的实现

merge函数是归并排序的灵魂。它接收两个已排序的子数组，并将它们合并成一个单一的有序数组。

  • 思路:
    1. 创建临时数组来存储合并后的结果。
    2. 使用三个指针，i指向第一个子数组，j指向第二个子数组，k指向临时数组。
    3. 比较arr[i]和arr[j]，将较小的元素放入临时数组，并移动相应的指针。
    4. 重复此过程，直到一个子数组被完全处理。
    5. 将另一个子数组中剩余的元素全部复制到临时数组。
    6. 最后，将临时数组的内容复制回原数组。

代码实现：归并排序

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
// Merge two subarrays of arr[].
// First subarray is arr[l..m]
// Second subarray is arr[m+1..r]
void merge(int arr[], int l, int m, int r) {
    int i, j, k;
    int n1 = m - l + 1;
    int n2 = r - m;

    // 创建临时数组
    int L[n1], R[n2];

    // 拷贝数据到临时数组
    for (i = 0; i < n1; i++) L[i] = arr[l + i];
    for (j = 0; j < n2; j++) R[j] = arr[m + 1 + j];

    // 合并临时数组回到原数组 arr[l..r]
    i = 0; j = 0; k = l;
    while (i < n1 && j < n2) {
        if (L[i] <= R[j]) {
            arr[k++] = L[i++];
        } else {
            arr[k++] = R[j++];
        }
    }

    // 拷贝L[]中剩余的元素
    while (i < n1) arr[k++] = L[i++];
    // 拷贝R[]中剩余的元素
    while (j < n2) arr[k++] = R[j++];
}

void mergeSort(int arr[], int l, int r) {
    if (l < r) {
        // 找到中点，避免 (l+r) 溢出
        int m = l + (r - l) / 2;

        // 递归排序左右两半
        mergeSort(arr, l, m);
        mergeSort(arr, m + 1, r);

        // 合并已排序的两半
        merge(arr, l, m, r);
    }
}
特性对比 快速排序 归并排序
平均时间 O(n log n) O(n log n)
最坏时间 O(n²) (需要优化) O(n log n)
空间复杂度 O(log n) (原地) O(n) (需额外空间)
稳定性 不稳定 稳定
适用场景 内部排序，对空间敏感 外部排序，对稳定性有要求

六：查找算法

查找（Search），是在数据集合中寻找特定元素的过程。看似简单的操作，在面对海量数据时，其效率直接决定了系统的响应速度和用户体验。不同的数据组织方式，催生了截然不同的查找策略。

12. 顺序查找：最朴素的策略

  • 思想: 从数据集合的第一个元素开始，逐一向后比对，直到找到目标或遍历完所有元素。这是一种“地毯式搜索”。
  • 时间复杂度: O(n)。在最坏情况下，需要检查集合中的每一个元素。
  • 适用场景:
    1. 数据无序且无法排序: 当数据本身是杂乱无章的，且没有条件或必要去排序时，顺序查找是唯一的选择。
    2. 数据量极小: 当n非常小时，O(n)的开销可以忽略不计，简单的顺序查找因其实现简单而成为首选。
    3. 链式存储结构: 对于单向链表，由于其不支持随机访问，通常也只能采用顺序查找。

[info] 工程视角

不要轻视顺序查找。在很多嵌入式系统或对代码尺寸有严格要求的场景中，如果数据量可控，一个简单、无依赖的for循环远比引入复杂的查找结构更具优势。“简单”本身就是一种强大的工程美学。

13. 二分查找 (Binary Search)：有序世界的利器

当数据集合有序且支持随机访问（如数组）时，二分查找展现出惊人的威力。

  • 思想: 通过不断将搜索区间折半，以对数级的速度逼近目标。每比较一次，就能排除掉一半的不可能选项。

二分查找动态过程
  • 时间复杂度: O(log n)。对于100万个数据，最多只需20次比较；对于10亿个数据，也仅需约30次。

难点攻克：二分查找的“魔鬼细节”与鲁棒实现

二分查找的原理简单，但完美实现却充满陷阱。高德纳（Donald Knuth）曾说：“虽然二分查找的基本思想相对简单，但细节可以非常棘手……第一个正确的二分查找算法在1946年就已出现，但第一个没有错误的实现直到1962年才发表。”

常见的陷阱：

  1. 整数溢出: 计算中点时，mid = (low + high) / 2 在low和high都很大时可能导致它们的和溢出。
  2. 死循环: 当区间更新逻辑不当时（如 low = mid 或 high = mid），在特定边界条件下可能导致搜索区间无法缩小，陷入死循环。
  3. 边界条件处理: 循环的终止条件是low < high还是low <= high？区间更新是high = mid还是high = mid - 1？这些微小的差异决定了算法的正确性。

实战代码：一个健壮的二分查找模板

这个模板通过精巧的边界设计，可以清晰地处理“查找特定值”、“查找第一个大于/等于某值的位置”等多种变体。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
#include <stdio.h>

/**
 * @brief 在一个升序数组中进行二分查找
 * @param arr 有序数组
 * @param len 数组长度
 * @param target 要查找的目标值
 * @return 如果找到，返回目标值的索引；如果未找到，返回-1。
 */
int binarySearch(int arr[], int len, int target) {
    if (arr == NULL || len <= 0) {
        return -1;
    }

    int low = 0;
    int high = len - 1;

    // 循环条件: low <= high
    // 当 low == high 时，区间还有一个元素，需要检查。
    // 当 low > high 时，区间为空，查找结束。
    while (low <= high) {
        // 防止溢出的中点计算方式
        int mid = low + (high - low) / 2;

        if (arr[mid] == target) {
            return mid; // 找到了！
        } else if (arr[mid] < target) {
            // 目标在右半部分，mid已经被检查过，所以新区间从 mid + 1 开始
            low = mid + 1;
        } else { // arr[mid] > target
            // 目标在左半部分，mid已经被检查过，所以新区间到 mid - 1 结束
            high = mid - 1;
        }
    }

    // 循环结束，low > high，说明未找到
    return -1;
}

int main() {
    int sorted_array[] = {2, 5, 8, 12, 16, 23, 38, 56, 72, 91};
    int n = sizeof(sorted_array) / sizeof(sorted_array[0]);
    int target1 = 23;
    int target2 = 15;

    int index1 = binarySearch(sorted_array, n, target1);
    int index2 = binarySearch(sorted_array, n, target2);

    if (index1 != -1) {
        printf("Target %d found at index: %d\n", target1, index1);
    } else {
        printf("Target %d not found.\n", target1);
    }

    if (index2 != -1) {
        printf("Target %d found at index: %d\n", target2, index2);
    } else {
        printf("Target %d not found.\n", target2);
    }

    return 0;
}

[info] 模板分析

  • 循环条件 low <= high: 保证了当搜索区间缩至单个元素时，该元素仍能被检查。
  • 区间更新 low = mid + 1 和 high = mid - 1: 确保每次循环都至少排除mid本身，从而保证了区间的严格缩小，避免死循环。

14. 分块查找：空间换时间的折中艺术

在无法对全部数据进行完全排序，但可以进行宏观分组的场景下，分块查找提供了一种优雅的性能提升方案。

  • 思想: 分块 + 索引。将大数据集分割成若干“块”，为这些块建立一个“索引表”。
➡️
从字典的部首检字法到分块查找

  • 结构:

    1. 数据块: 原始数据被划分为连续的块。块内元素可以无序，但块间必须有序（例如，第 i+1 块的所有元素都大于第 i 块的所有元素）。
    2. 索引表: 一个小数组，每个条目对应一个数据块，存储该块的关键信息（通常是块内最大值）和起始地址/索引。

  • 查找过程:

    1. 第一步：在索引表中查找。由于索引表本身是有序且数据量小，可以使用二分查找（或顺序查找）快速定位目标值可能所在的块。
    2. 第二步：在数据块内查找。进入定位到的数据块，在块内进行顺序查找。

  • 性能分析: 设数据总量为n，分为b块，则每块大小为n/b。索引查找时间为O(log b)（用二分法），块内查找时间为O(n/b)。总时间复杂度为 O(log b + n/b)。通过调整块的数量b，可以在时间和空间（索引表大小）之间找到平衡点。当b = sqrt(n)时，可以取得较好的理论性能。

工程价值与适用场景

分块查找的真正价值在于它对数据容忍了一定程度的无序，非常适合处理动态变化的数据集。

  • 场景: 数据库索引。数据库的表数据在物理上可能不是完全有序的（因为增删改），但数据库会维护一个B+树索引（一种高级的多路分块结构）。查找时，先通过索引快速定位到包含目标数据的数据页（块），然后再在数据页内查找。这使得在海量动态数据中进行高效查找成为可能。
  • 优点: 在插入新数据时，只需找到对应的块并插入，无需像维护一个完全有序数组那样移动大量数据。它在查找效率和维护成本之间取得了出色的平衡。

15. 哈希查找 ：O(1) 的理想与现实

前面所有查找算法，都离不开“比较”。而哈希查找另辟蹊径，试图通过一次计算就直接定位到数据。

  • 思想:

    1. 哈希函数 (Hash Function): 设计一个函数 h(key)，它能将任意的关键字key映射到一个固定范围的整数，这个整数就是数据在哈希表（通常是一个数组）中的存储位置（索引）。
    2. 哈希表 (Hash Table): 一个数组，用于存储数据。
    3. 查找: 当要查找一个key时，只需计算 index = h(key)，然后直接访问哈希表的 index 位置即可。

  • 时间复杂度: 理想情况下，每次查找只需一次哈希计算和一次数组访问，时间复杂度为 O(1)。

难点攻克：哈希冲突

理想是丰满的，现实是骨感的。不同的key通过哈希函数可能会计算出相同的index，这就是哈希冲突。

  • 例子: h(key) = key % 10。h(12) 和 h(22) 都会得到索引 2。

解决冲突的常用方法：

  1. 开放定址法 (Open Addressing): 如果计算出的位置已被占用，就按照某种规则（线性探测、二次探测等）去寻找下一个空位。
  2. 链地址法 (Chaining): （最常用）哈希表的每个位置不再是单个元素，而是一个链表的头指针。所有哈希到同一位置的元素，都以节点的形式挂载到这个链表上。查找时，先计算哈希值定位到链表，再在链表上进行顺序查找。

链地址法解决哈希冲突

性能总结与对比

查找算法 数据要求 平均时间复杂度 最坏时间复杂度 空间复杂度
顺序查找 无 O(n) O(n) O(1)
二分查找 有序, 随机访问 O(log n) O(log n) O(1)
分块查找 块间有序 O(log b + n/b) O(log b + n/b) O(b)
哈希查找 无 O(1) O(n) (全冲突) O(n)

最终洞察:

  • 没有最好的算法，只有最合适的算法。
  • 二分查找是静态有序数据集的王者。
  • 哈希查找是追求极致查询速度（尤其是动态数据集）的首选，但以额外的空间和哈希函数设计为代价。
  • 分块查找和其衍生（如B树）是在查找效率和动态维护成本之间寻求平衡的工程典范，是大型数据库和文件系统的基石。
数据结构与算法
许可协议

本文采用 署名-非商业性使用-相同方式共享 4.0 国际 许可协议，转载请注明出处。

分享文章